www.slide4math.com

This is my version of explanation. I would suggest you to come up with your own explanation. The best way would be for you to try explain this to somebody else in your own words.

Following is my version of explanation, but this is just an example. You may come up with a better version.

Combining the exponential function with real value exponent and the one with the complex number exponent

  - Increasing Magnitude -

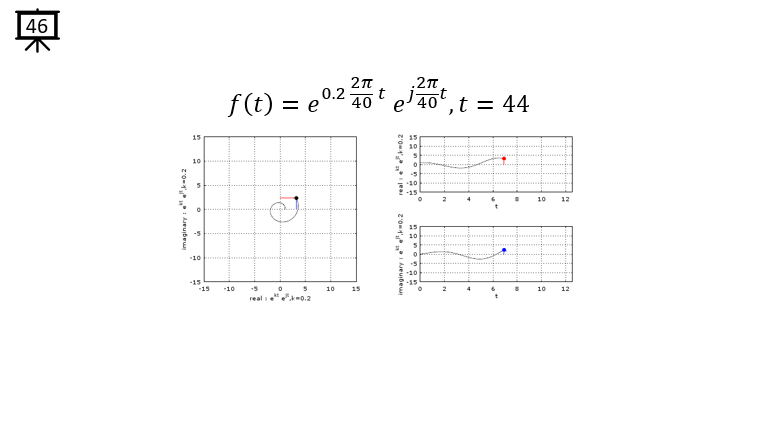
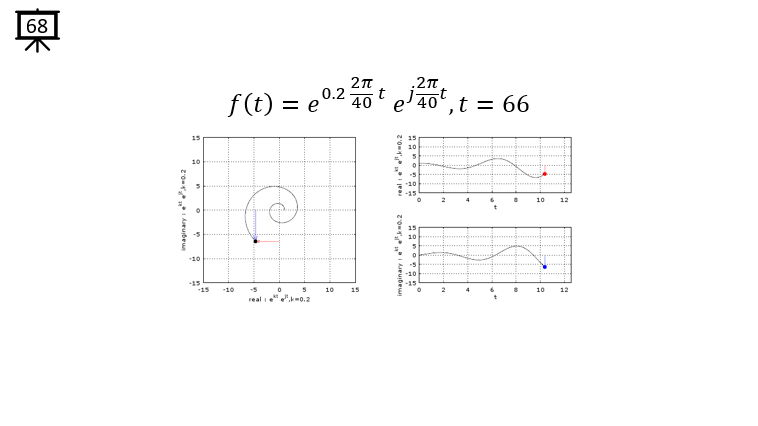
Followings are the code that I wrote in Octave to creates all the plots shown in this page. You may copy these code and play with these codes. Change variables and try yourself until you get your own intuitive understanding.

< Code 1 >

tstep = 2*pi/40;

%t=0:tstep:tstep*40*2;

t=0:tstep:tstep*80;

k=1;

k1 = 0.2;

k2 = 1;

d=0;

e = exp(k1*t) .* exp(k2*t*j);

stateDiagramAxis = [-15 15 -15 15];

realAxis = [0 4*pi -15 15];

imagAxis = [0 4*pi -15 15];

maxHeadSize = 0.1;

hFig = figure(1);

subplot(2,2,2);

plot(t,real(e),'k-');

axis(realAxis);

xlabel('t');ylabel('real : e^{kt} e^{jt},k=-0.2');

grid on;

hold on;

plot(t(end),real(e(end)),'ro',"markerfacecolor",[1 0 0]);

quiver([t(end)],[0],[0],[real(e(end))],"color","red","maxheadsize", maxHeadSize);

hold off;

subplot(2,2,4);

plot(t,imag(e),'k-');

axis([imagAxis]);xlabel('t');ylabel('imaginary : e^{kt} e^{jt},k=-0.2');

grid on;

hold on;

plot(t(end),imag(e(end)),'bo',"markerfacecolor",[0 0 1]);

quiver([t(end)],[0],[0],[imag(e(end))],"color","blue","maxheadsize", maxHeadSize);

hold off;

subplot(2,2,[1 3]);

plot(real(e),imag(e),'k-');

axis(stateDiagramAxis);xlabel('real : e^{kt} e^{jt},k=-0.2');ylabel('imaginary : e^{kt} e^{jt},k=-0.2');

grid on;

hold on;

plot(real(e(end)),imag(e(end)),'ko',"markerfacecolor",[0 0 0]);

quiver([real(e(end))],[0],[0],[imag(e(end))*1.1],"color","blue","maxheadsize", maxHeadSize);

quiver([0],[imag(e(end))],[real(e(end))*1.1],[0],"color","red","maxheadsize", maxHeadSize);

hold off;

pos = [(i/50.0) 0.01 (1.0/50.0) 0.98];

set(hFig,'Position',[300 400 800 300])