www.slide4math.com

This is my version of explanation. I would suggest you to come up with your own explanation. The best way would be for you to try explain this to somebody else in your own words.

Following is my version of explanation, but this is just an example. You may come up with a better version.

Example of Vector Field - Two Charges

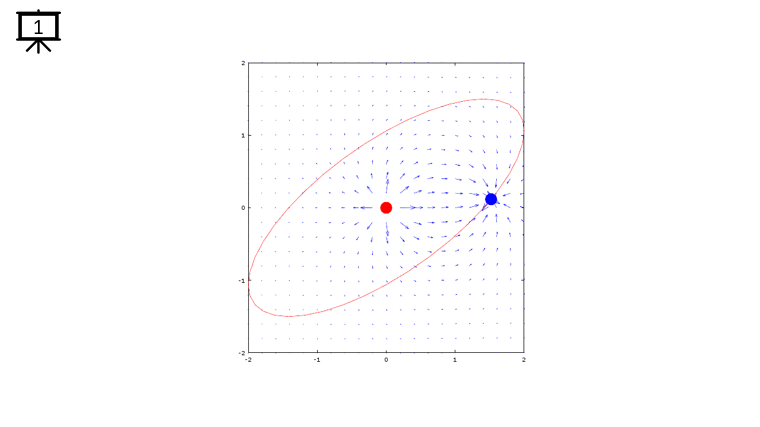
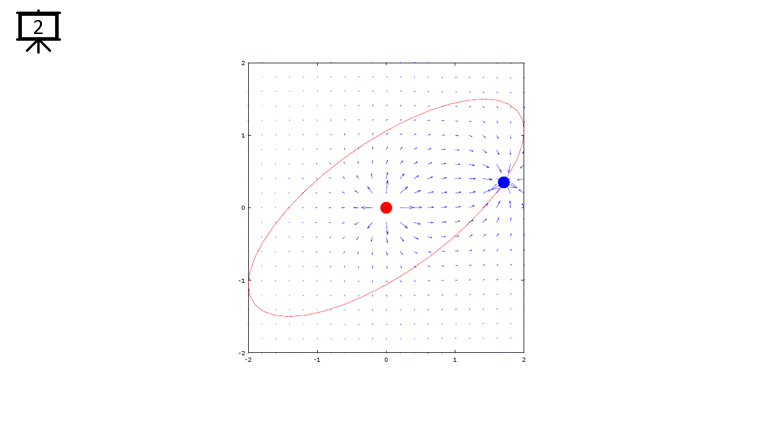
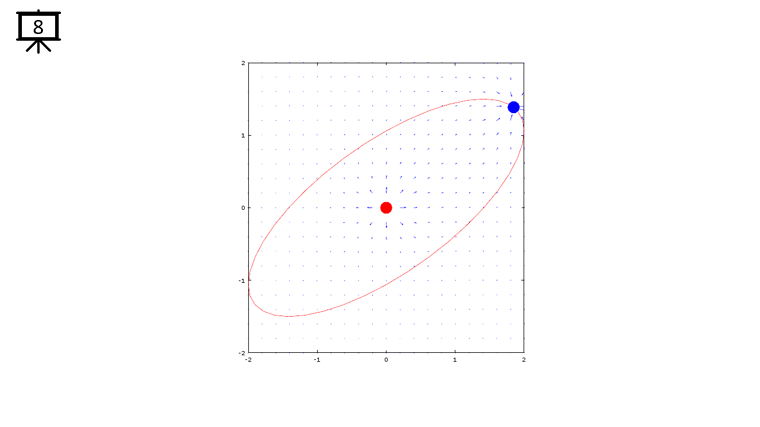
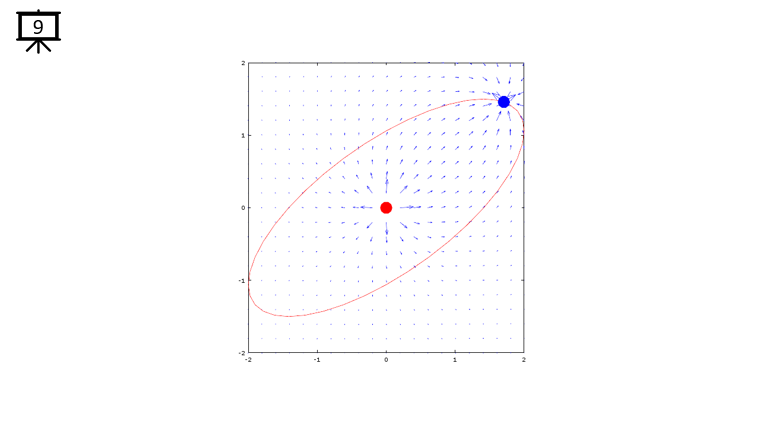
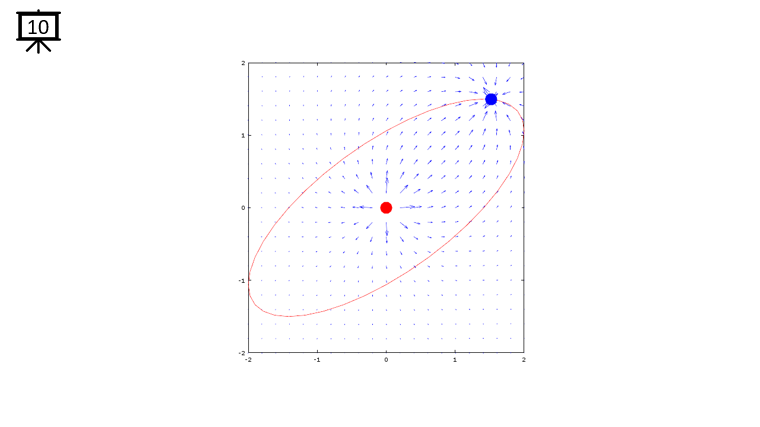
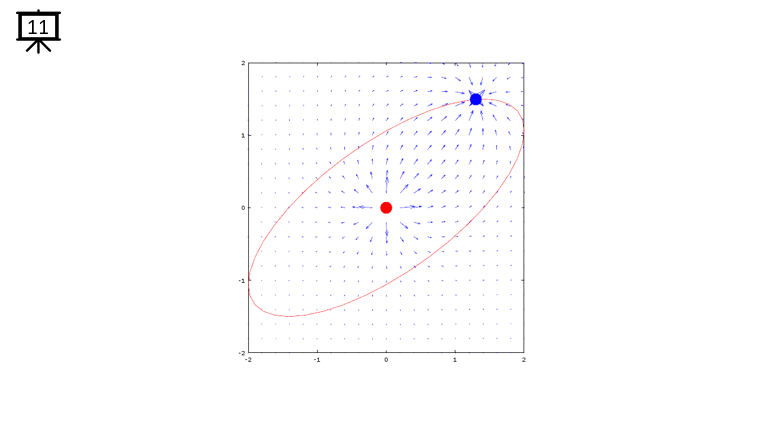
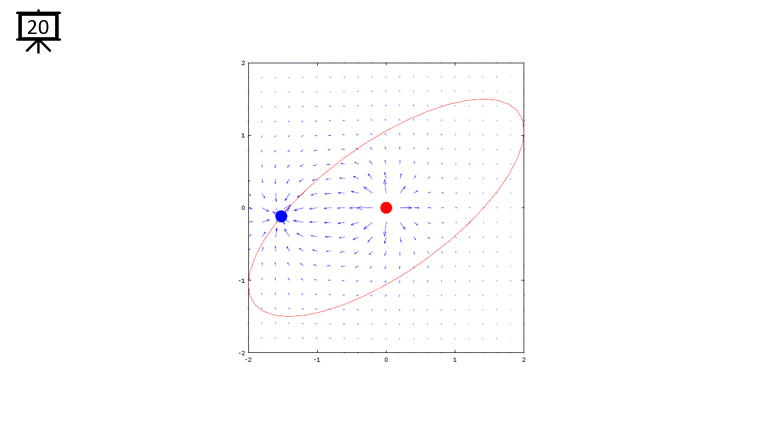
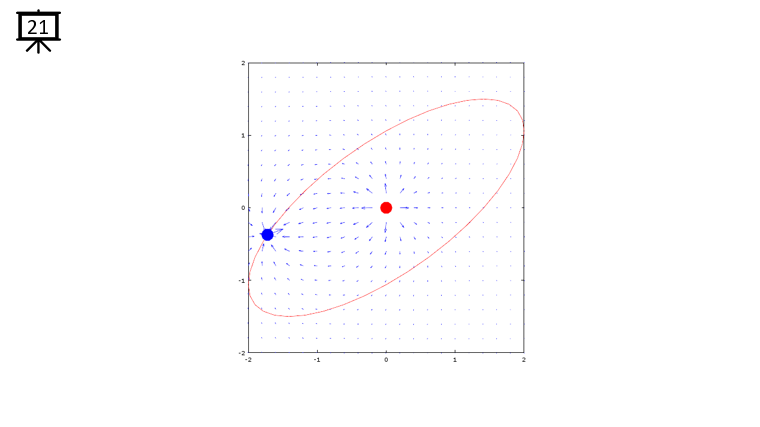
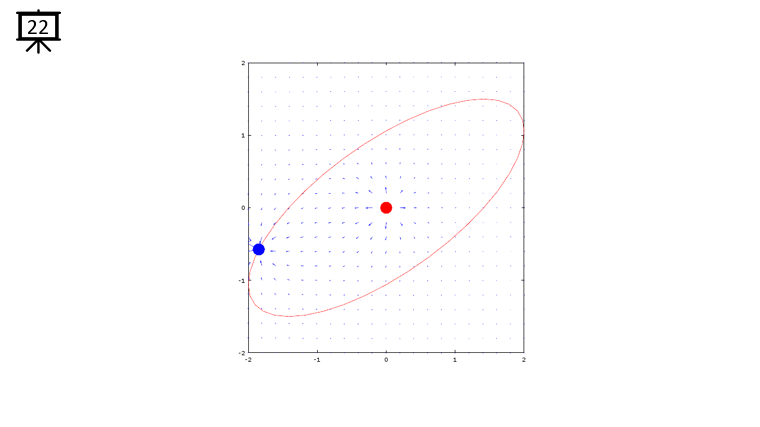
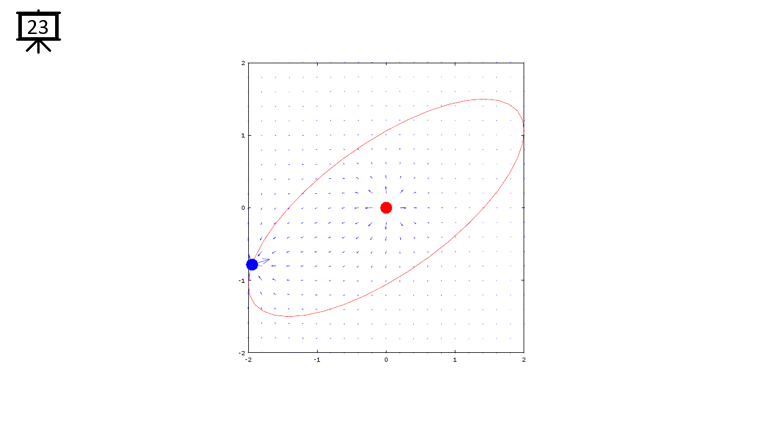
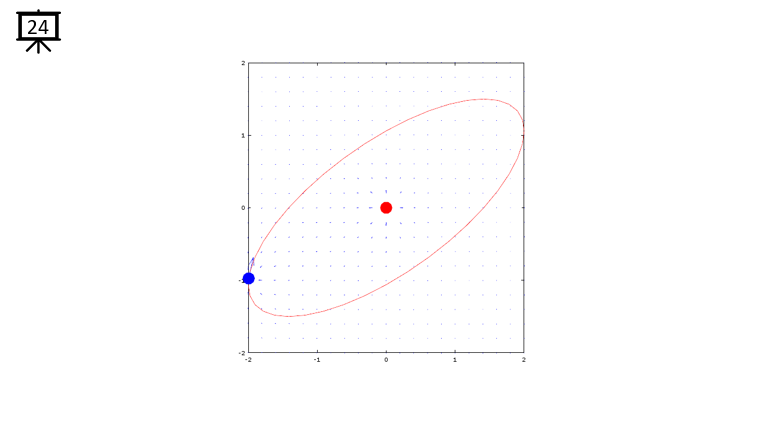
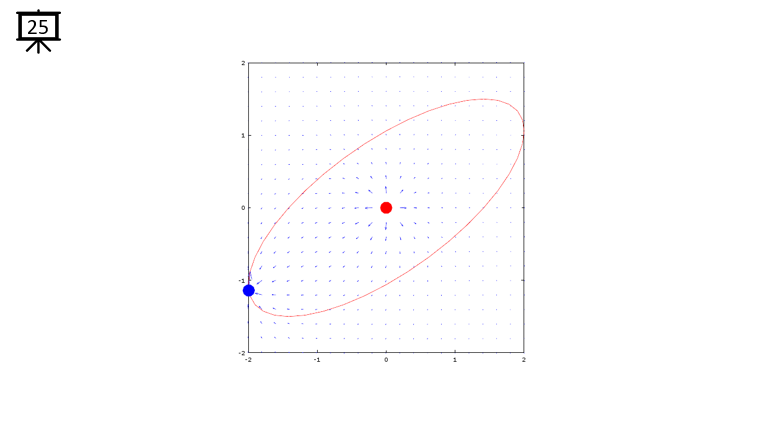
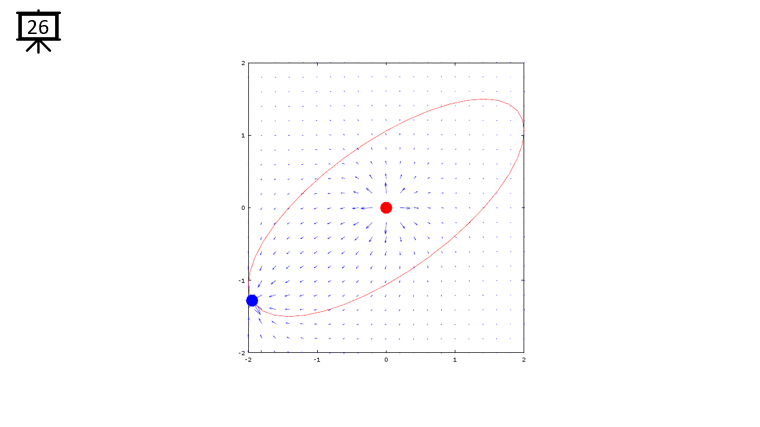
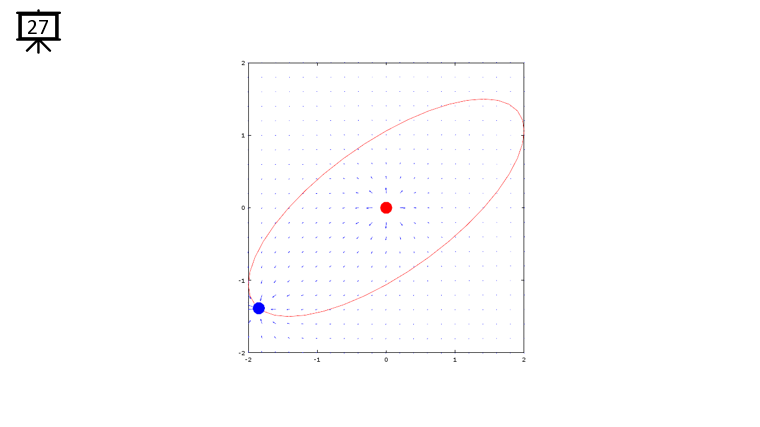
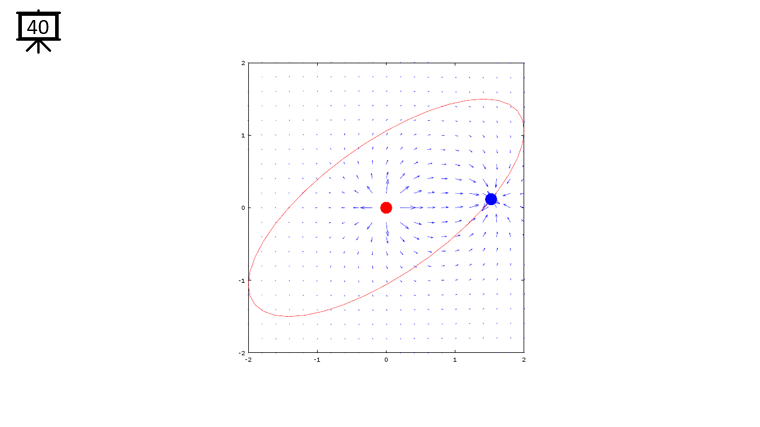
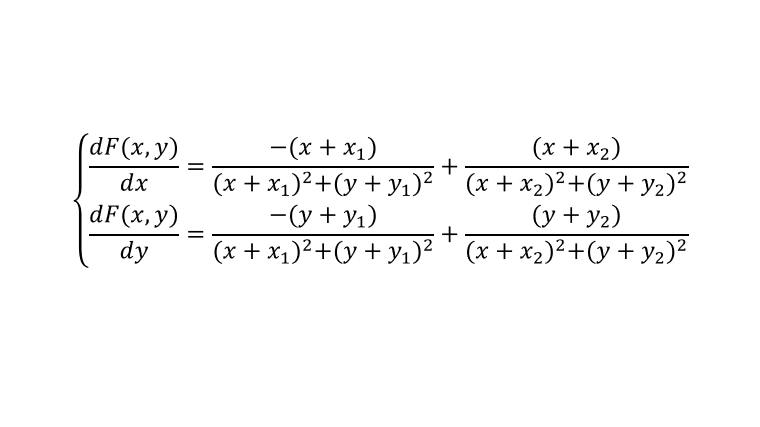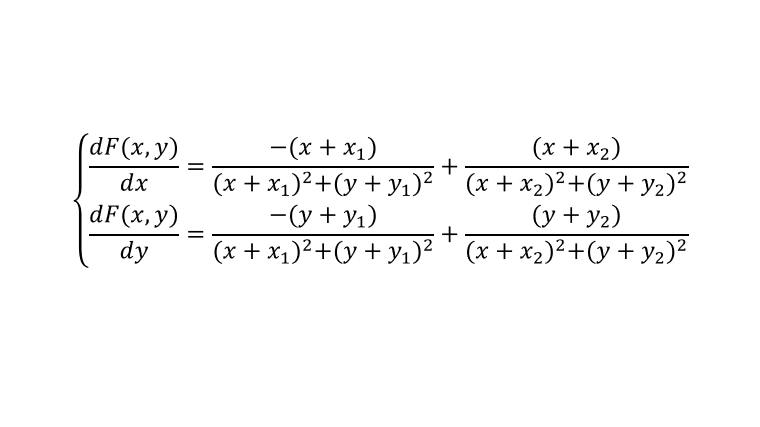Followings are the code that I wrote in Octave to creates all the plots shown in this page. You may copy these code and play with these codes. Change variables and try yourself until you get your own intuitive understanding.

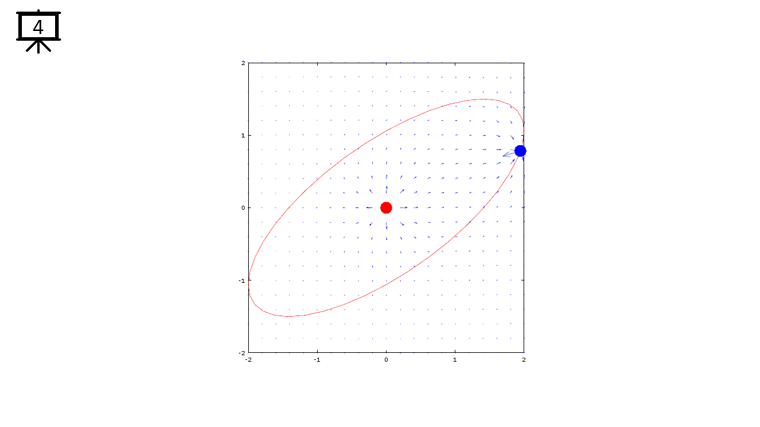
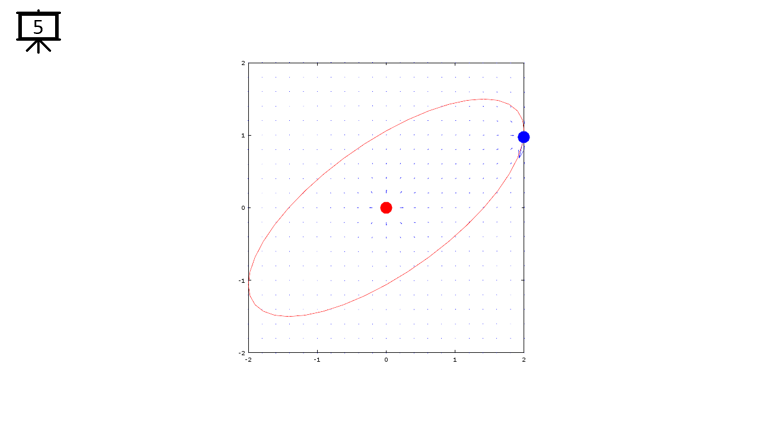
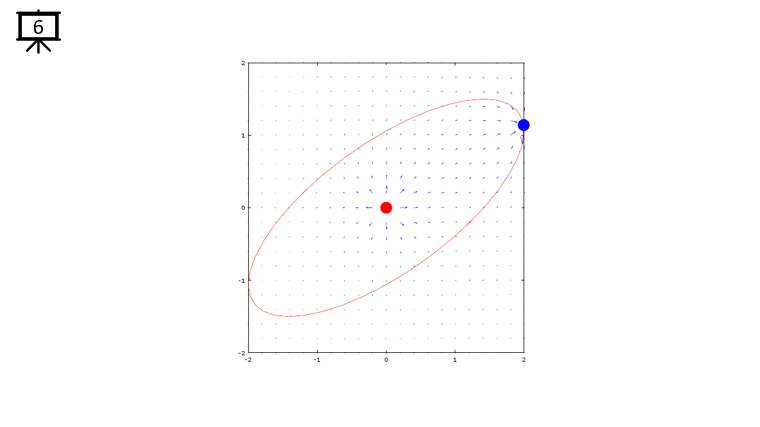
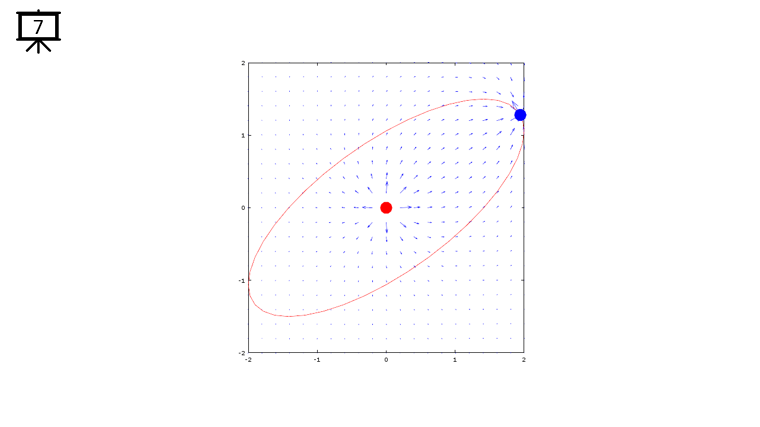
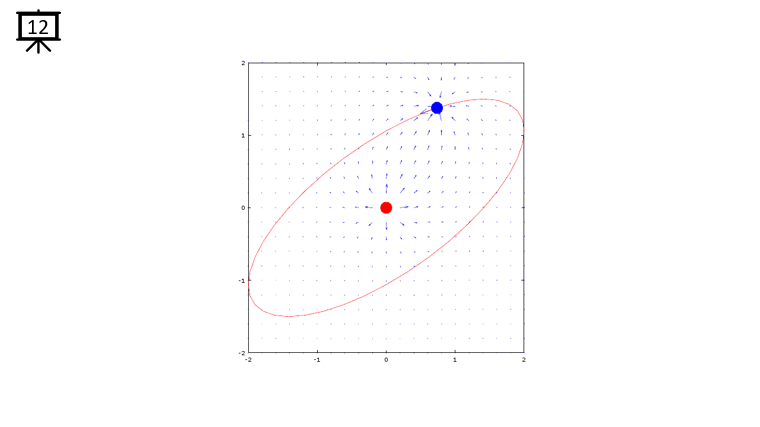
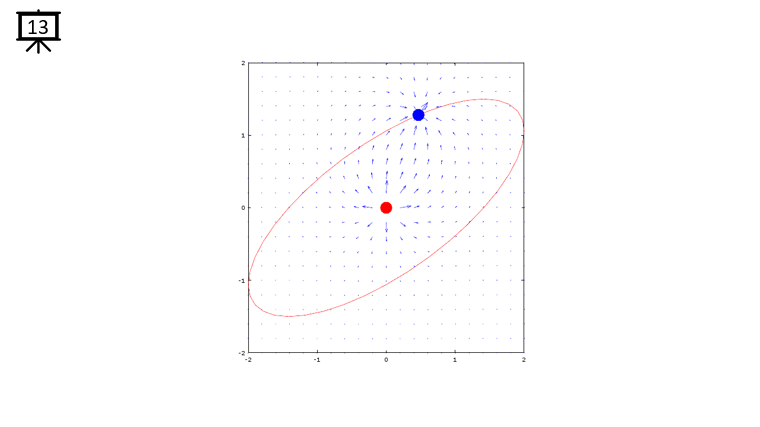
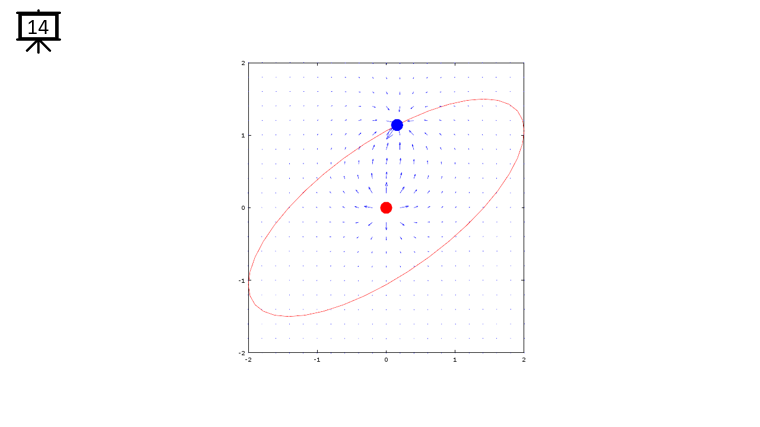
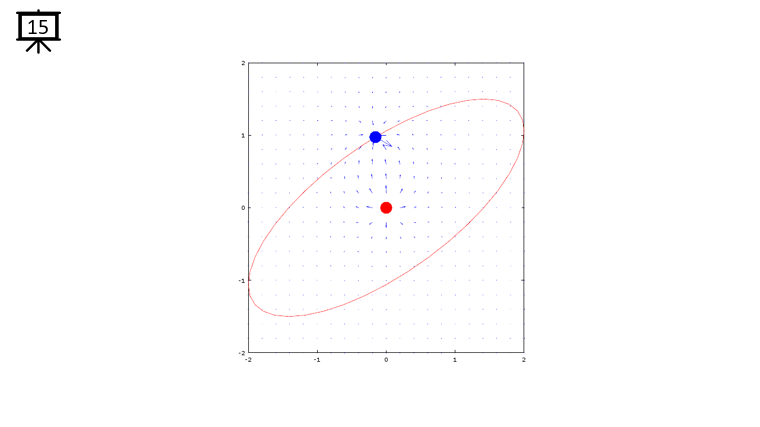
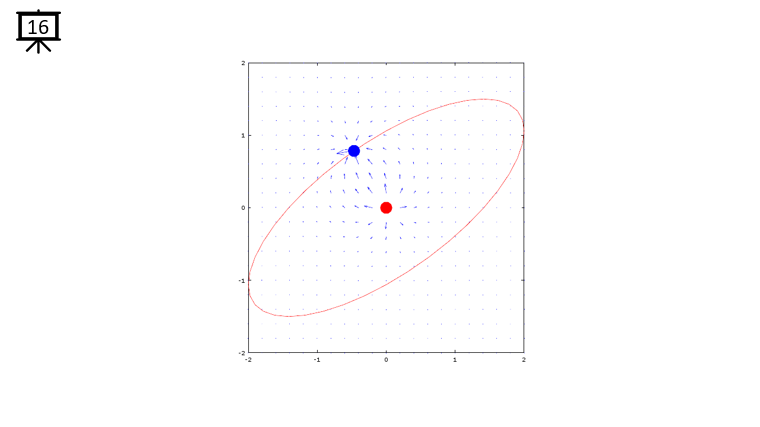
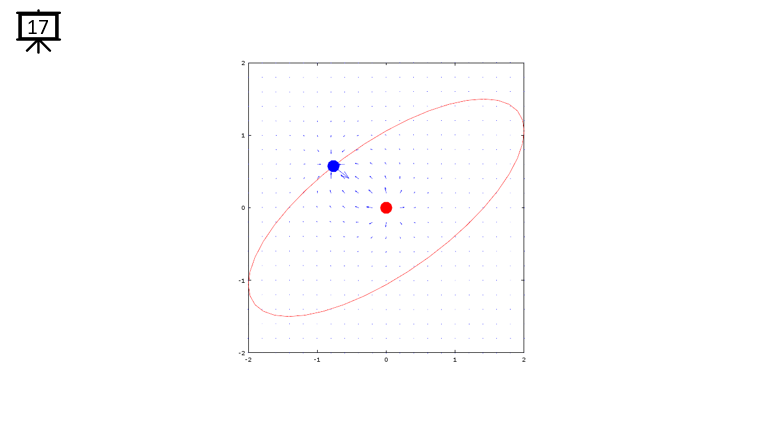
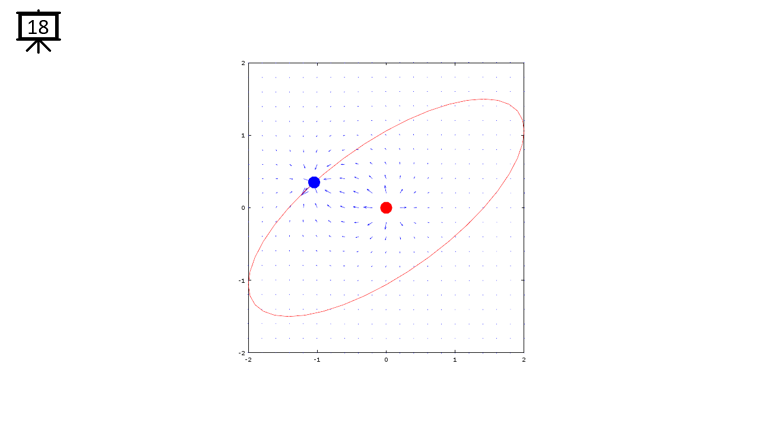
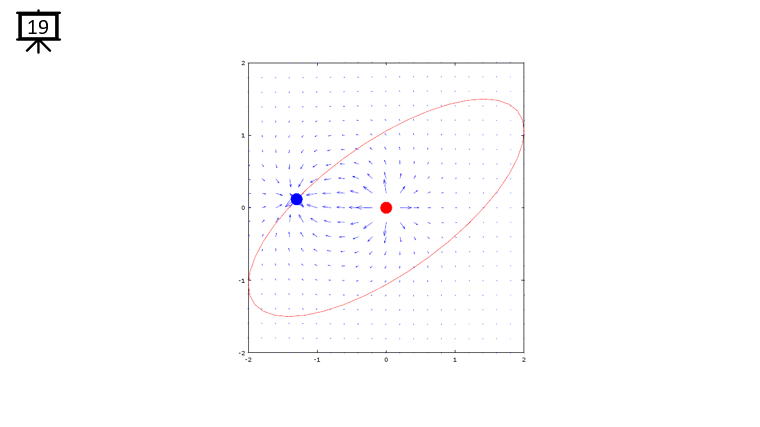
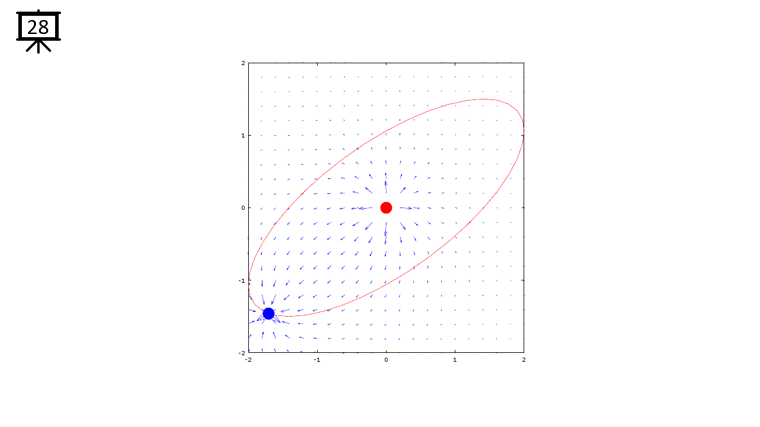
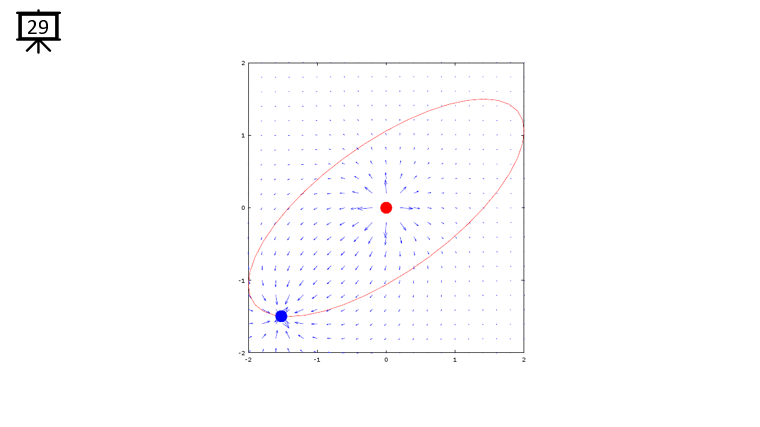
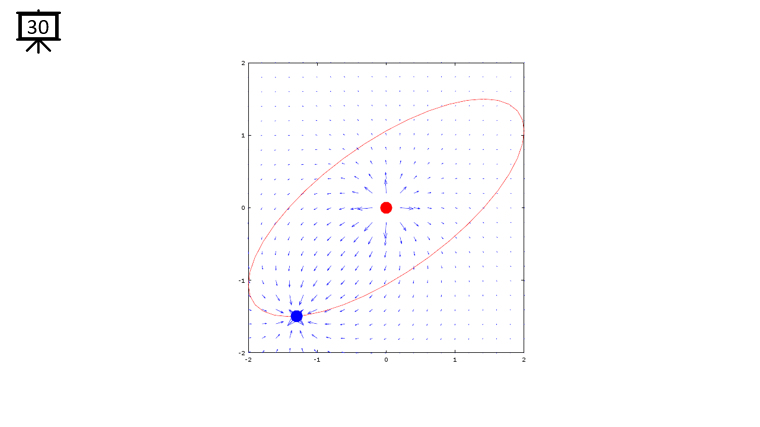
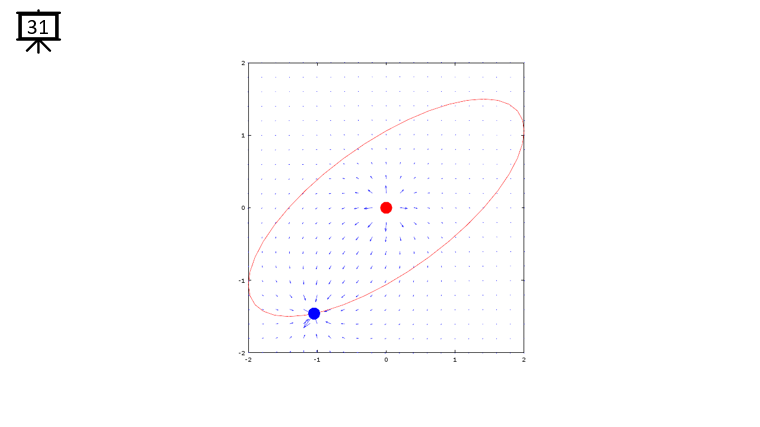
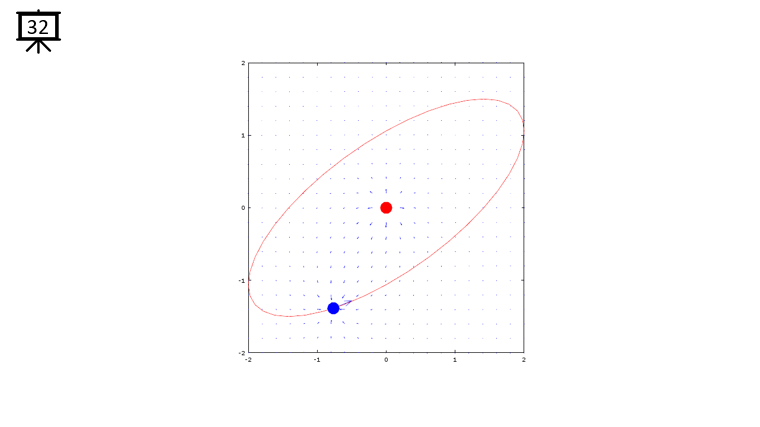
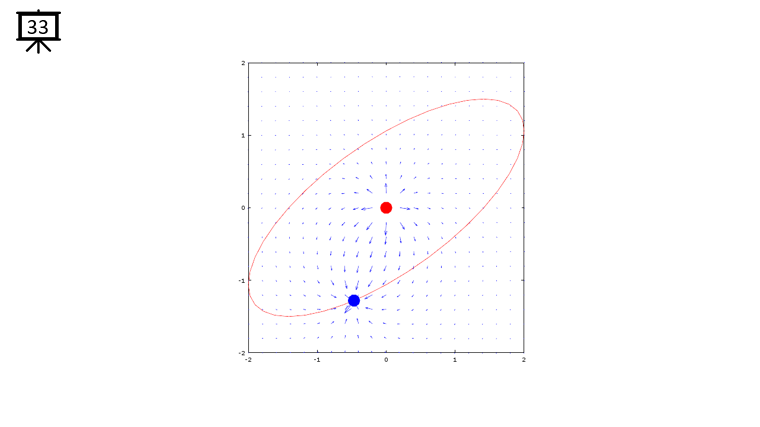
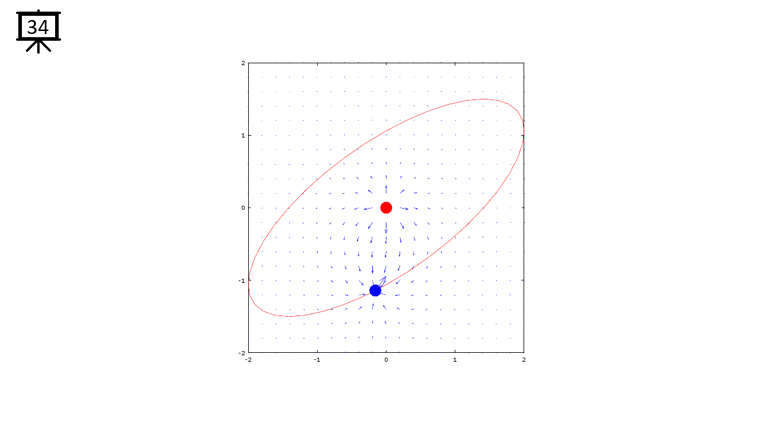
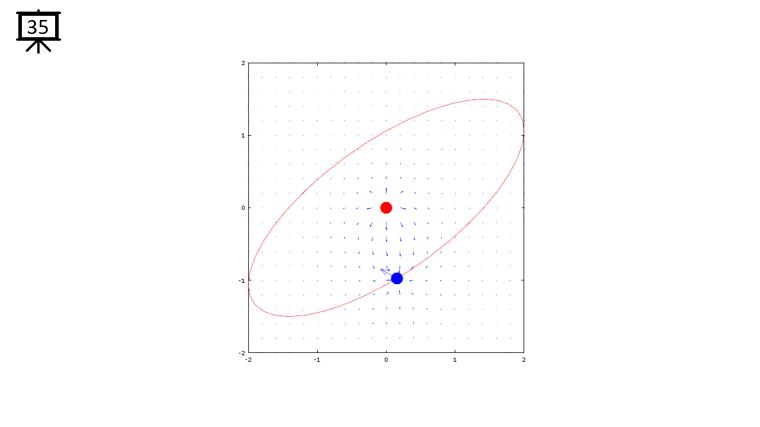
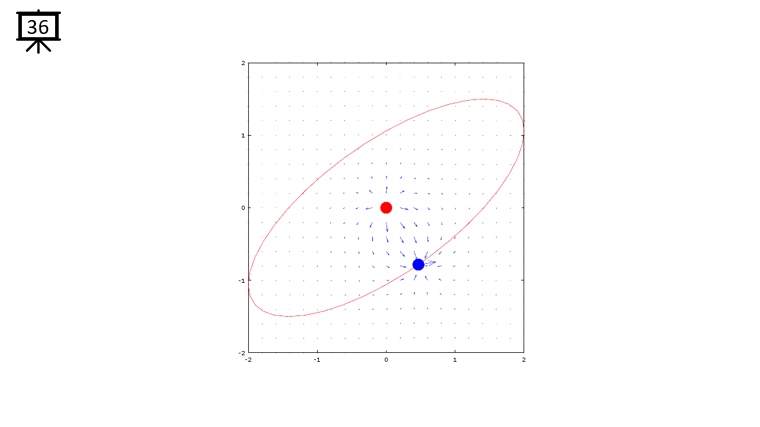
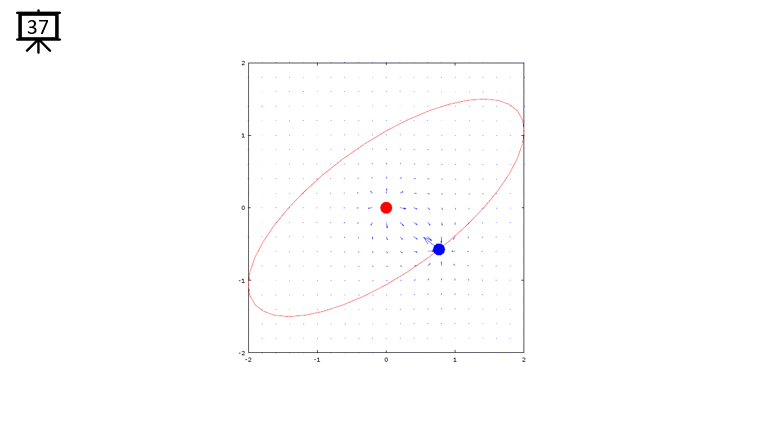
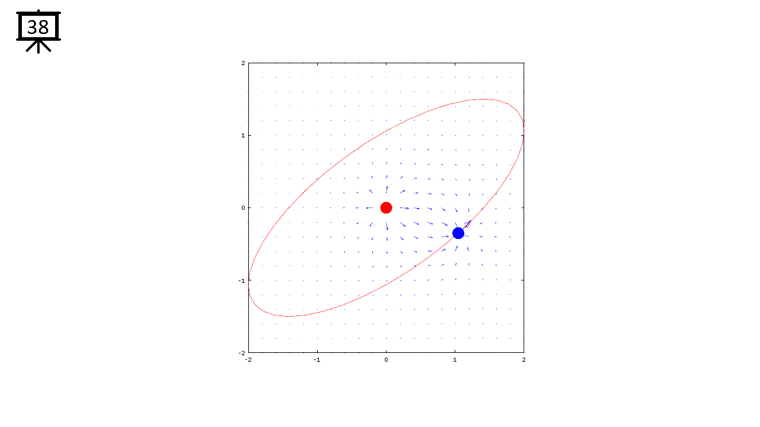
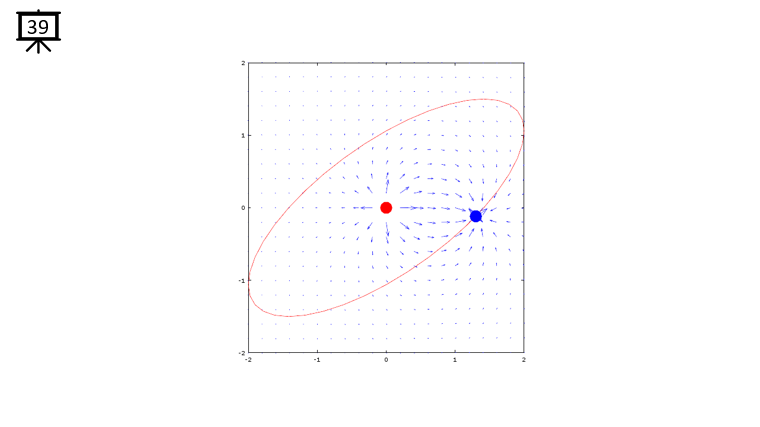
< Code 1 >

v = -2:0.2:2;  % you can change the range to best fit the plot

th = 0:pi/20:2*pi;

xth = 2*cos(th-pi/4);

yth = 1.5*sin(th);

t0 = (0.5+40.0) * pi/20;

a = -1;

b = 1;

c = -1;

d = 1;

x1 = -2*cos(t0-pi/4);

x2 = 0;

y1 = -1.5*sin(t0);

y2 = 0;

[x,y] = meshgrid(v);

dx= a .* (x+x1) ./ ((x+x1) .^2 + (y+y1) .^2) + b .* (x+x2) ./ ((x+x2) .^2 + (y+y2) .^2);

dy= c .* (y+y1) ./ ((x+x1) .^2 + (y+y1) .^2) + d .* (y+y2) ./ ((x+x2) .^2 + (y+y2) .^2);

hFig = figure(1);

hold on;

quiver(x,y,dx,dy,1.2);

plot(-x2,-y2,'ro','MarkerFaceColor',[1 0 0],'MarkerSize',20);

plot(-x1,-y1,'bo','MarkerFaceColor',[0 0 1],'MarkerSize',20);

plot(xth,yth,'r-');

axis([-2 2 -2 2]);

hold off;

set(hFig,'Position',[300 100 600 600]);